💻 Romlig utvelgelse

💻 Romlig utvelgelse#

Open In Colab

En vanlig oppgave når man jobber med romlige data er utføre ulike GIS-operasjoner basert på hvordan ulike data er plassert i forhold til hverandre. For eksempel er det svært vanlig å finne ut om et bestemt punkt er lokalisert innenfor et område, eller om en linje krysser en annen linje eller en polygon, for å velge data basert på romlig plassering. Alt dette går under det man kan kalle romlig utvelgelse. Romlige utvelgelser utføres basert på topologiske romlige relasjoner, som er grunnleggende konstruksjoner som beskriver hvordan to eller flere geometriske objekter forholder seg til hverandre med hensyn til deres posisjon og grenser.

Du kan lese mer om de topologiske sammenhengene i kapittel 6.6 i Python for Geographic Data Analysis, men for vårt formål her er figuren under en oversikt over de underliggende romlige dimensjonene til de ulike romlige objektene vi jobber med:

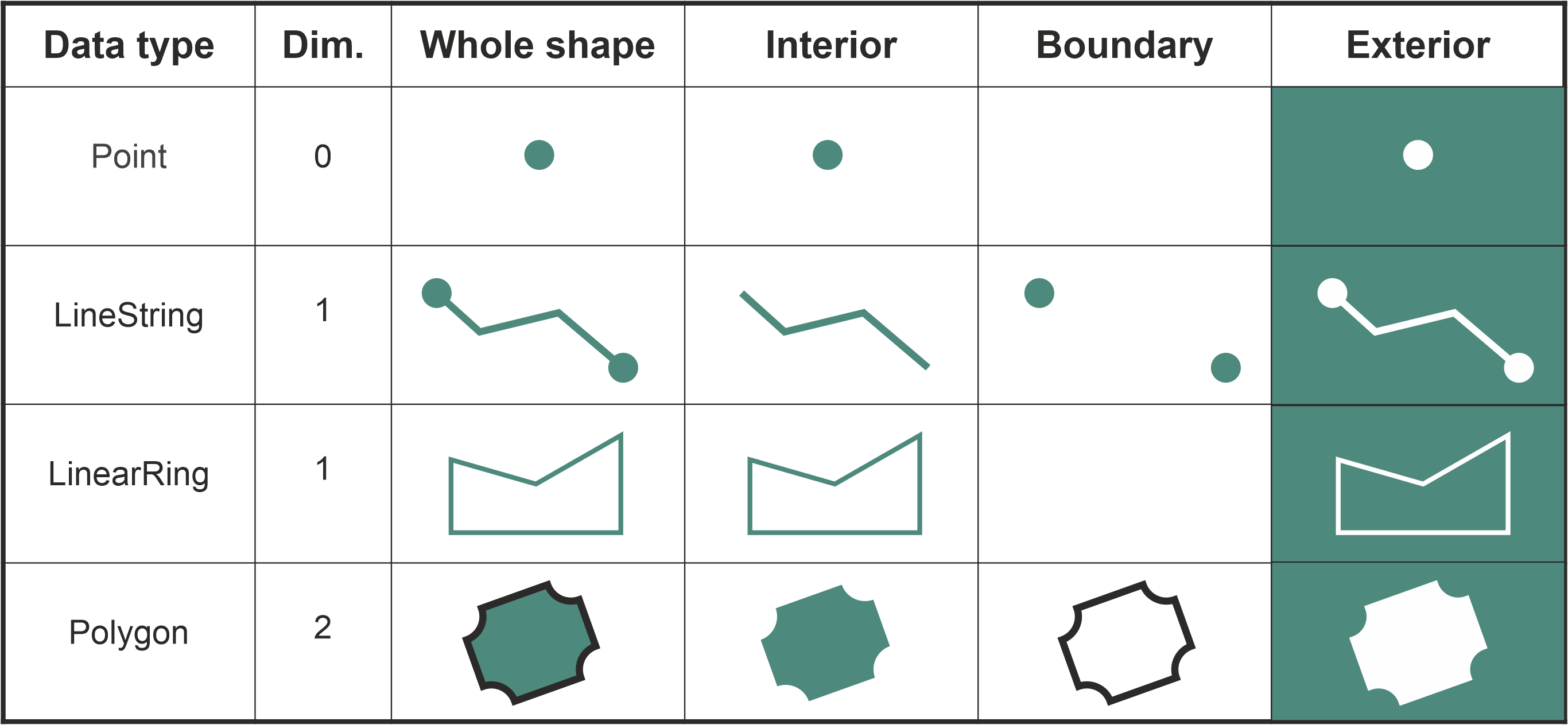
Romlige dimensjoner

Romlige predikater#

Når vi i GIS-analyser tester hvordan ulike geometriske objekter forholder seg til hverandre, får man et resultat som kalles et romlig predikat. De vanligste romlige predikatene er vist i figuren under og mange av disse predikatene, som intersects, within, contains, overlaps og touches, brukes ofte når man velger data for et spesifikt interesseområde eller når man kobler data fra ett datasett til et annet basert på den romlige relasjonen mellom lagene.

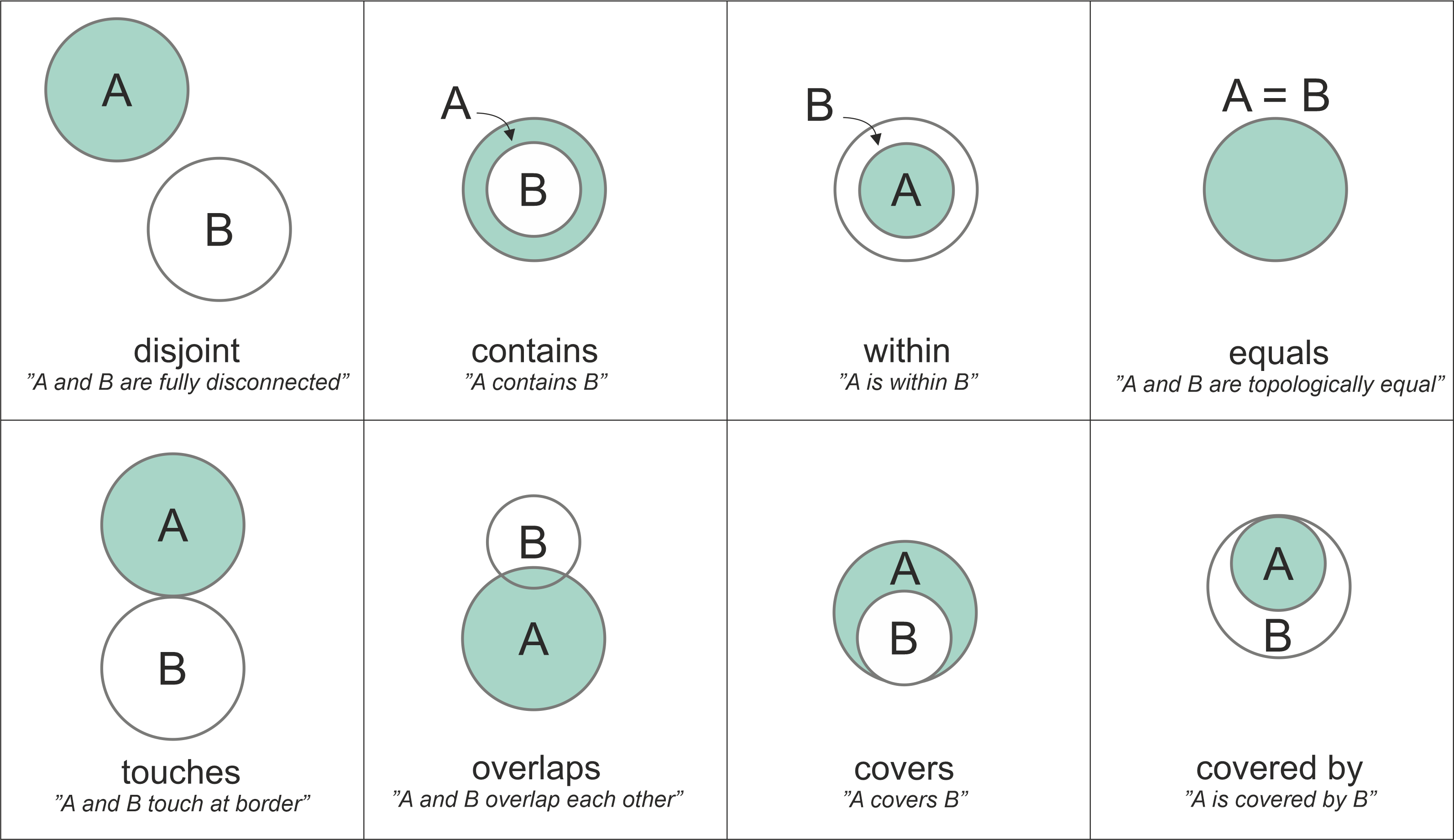
Romlige predikater

Den øverste raden i figuren viser romlige predikater der geometriene A og B er klart adskilt fra hverandre, inneholder eller er innenfor hverandre, eller er identiske med hverandre. Når geometriene har minst ett punkt til felles, sies det at geometriene intersects (skjærer) hverandre. Dermed er alle sammenligningene i denne figuren, bortsett fra den første (disjoint), sanne, dvs. geometriene skjærer hverandre.

Den nederste raden viser eksempler på romlige forhold som på en eller annen måte er litt “spesialtilfeller”. Når to geometriske objekter berører hverandre, har de minst ett punkt til felles (ved yttergrensengrensen i dette tilfellet), men deres indre skjærer ikke hverandre. Når det indre av geometriene A og B delvis er oppå hverandre og delvis utenfor hverandre, overlapper geometriene hverandre. Det romlige predikatet for covers er når interiøret til geometri B nesten er helt innenfor A, men de deler minst én felles koordinat ved grensen. Tilsvarende, hvis geometri A nesten er helt inneholdt av geometri B (bortsett fra minst ett felles koordinat ved grensen), kalles det romlige predikatet covered by. Disse åtte eksemplene representerer noen av de vanlige romlige predikatene basert på to polygonformer.

Romlig utvelgelse i Python#

Når vi skal utføre romlige utvelgelser i Python er disse heldigvis allerede implementert i shapely og geopandas. Med disse bibliotekene kan vi enkelt og effektivt evaluere den topologiske relasjonen mellom geometriske objekter. I Python er alle de grunnleggende romlige predikatene tilgjengelige fra shapely-biblioteket, inkludert:

  • .intersects()

  • .within()

  • .contains()

  • .overlaps()

  • .touches()

  • .covers()

  • .covered_by()

  • .equals()

  • .disjoint()

  • .crosses()

Vi har allerede tidligere sett på hvordan .intersects() fungerer, så la oss nå utføre en punkt i polygon-analyse.

Punkt i polygon-analyse#

Å finne ut om et bestemt punkt er plassert innenfor eller utenfor et område, eller å finne ut om en linje krysser en annen linje eller polygon er grunnleggende romlige spørringer som ofte brukes f.eks. for å velge data basert på plassering. Slike romlige spørringer er en av de typiske første trinnene i arbeidsflyten når du gjør romlig analyse. Å utføre en romlig kobling (vil bli introdusert senere) mellom to romlige datasett er en av de mest typiske bruksområdene der Punkt-i-Polygon (PIP)-analyser brukes.

For videre lesing om PIP og andre geometriske operasjoner, se kapittel 4.2 i Smith, Goodchild & Longley: Geospatial Analysis - 6th edition.

Hvordan sjekke om et punkt er inne i en polygon?#

Beregningsteknisk er det mest vanlig å oppdage om et punkt er inne i en polygon ved å bruke en spesifikk formel kalt Ray Casting-algoritmen. Heldigvis trenger vi ikke å lage en slik funksjon selv for utføre Punkt-i-Polygon (PIP)-analyser. I stedet kan vi dra fordel av Shapely’s binære predikater som kan evaluere de topologiske forholdene mellom geografiske objekter, så som PIP, som vi er interessert i her.

Spørringer om punkt-i-polygon på shapely geometrier#

Det er stort sett to måter å utføre PIP på i Shapely:

  1. ved hjelp av en funksjon kalt within() som sjekker om et punkt er innenfor et polygon

  2. ved hjelp av en funksjon kalt contains() som sjekker om et polygon inneholder et punkt

Note

Selv om vi snakker her om Point i Polygon operasjon, er det også mulig å sjekke om en LineString eller Polygon er inne i et annen Polygon.

La oss først lage et par punktgeometrier:

import shapely.geometry
punkt1 = shapely.geometry.Point(24.952242, 60.1696017)
punkt2 = shapely.geometry.Point(24.976567, 60.1612500)

… og en polygon:

polygon = shapely.geometry.Polygon(
    [
        (24.950899, 60.169158),
        (24.953492, 60.169158),
        (24.953510, 60.170104),
        (24.950958, 60.169990)
    ]
)

print(punkt1)
print(punkt2)
print(polygon)

POINT (24.952242 60.1696017)
POINT (24.976567 60.16125)
POLYGON ((24.950899 60.169158, 24.953492 60.169158, 24.95351 60.170104, 24.950958 60.16999, 24.950899 60.169158))

La oss sjekke om punktene er within() polygonet:

punkt1.within(polygon)

True

punkt2.within(polygon)

False

Det ser ut til at det første punktet er inne i polygonet, men det andre er ikke det.

Vi kan snu logikken til spørringen: I stedet for å sjekke om punktet er innenfor polygonet, kan vi også spørre om polygonet contains() punktet:

polygon.contains(punkt1)

True

polygon.contains(punkt2)

False

Hint

De to måtene å sjekke det romlige forholdet er komplementære og gir ekvivalente resultater; contains() er invers av within(), og omvendt.

Så, hvilken skal du bruke? Vel, det avhenger av:

  • hvis du har mange punkter og bare ett polygon og du prøver å finne ut hvilket av dem som er inne i polygonet: Da må du kanskje iterere over punktene og sjekke ett om gangen om det er within() polygonet.

  • hvis du har mange polygoner og bare ett punkt og du vil finne ut hvilket polygon som inneholder punktet: Da må du kanskje iterere over polygonene til du finner et polygon som contains() det spesifiserte punktet

Spørringer om punkt-i-polygon på geopandas.GeoDataFrames#

I det følgende praktiske eksempelet finner vi ut hvilke av adressene vi fikk i geokodingseksjonen som ligger innenfor en bestemt bydel i Oslo.

import pathlib
NOTEBOOK_PATH = pathlib.Path().resolve()
DATA_MAPPE = NOTEBOOK_PATH / "data"

import geopandas

bydeler = geopandas.read_file(
    DATA_MAPPE / "oslo_bydeler" / "oslo_bydeler_befolkning_2024.geojson"
)
bydeler.head()
fid bydelsnr bynavn bydel befolkning_2024 geometry
0 1 030101 Oslo Gamle Oslo 63721 MULTIPOLYGON (((10.66087 59.88365, 10.66472 59...
1 2 030102 Oslo Grünerløkka 65532 MULTIPOLYGON (((10.75378 59.91469, 10.75453 59...
2 3 030103 Oslo Sagene 47627 MULTIPOLYGON (((10.77156 59.93095, 10.77135 59...
3 4 030104 Oslo St.Hanshaugen 41571 MULTIPOLYGON (((10.75136 59.91923, 10.75158 59...
4 5 030105 Oslo Frogner 60727 MULTIPOLYGON (((10.65562 59.89038, 10.65381 59... 
bydeler.plot()

<Axes: >
../../_images/58216ddfb3a8162ec96d97ac63164e98164dfbfef359a9e06665744c2457e076.png

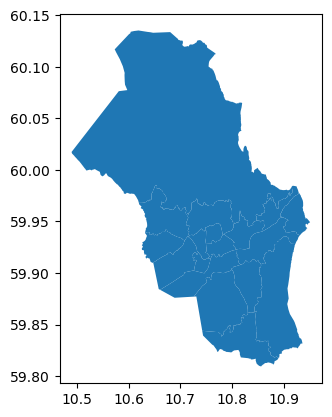
Spesielt ønsker vi å finne ut hvilke punkter som er innenfor bydelen “Gamle Oslo”. La oss begynne med å få et separat datasett for denne bydele, laste in adressene, og plotte et flerlagskart som viser alle bydelene, “Gamle Oslo” og alle punktene i ett kart:

gamle_oslo = bydeler[bydeler.bydel == "Gamle Oslo"]
gamle_oslo
fid bydelsnr bynavn bydel befolkning_2024 geometry
0 1 030101 Oslo Gamle Oslo 63721 MULTIPOLYGON (((10.66087 59.88365, 10.66472 59... 
adresser = geopandas.read_file(DATA_MAPPE / "oslo_adresser" / "adresser.geojson")

Plotting av flere kartlag

For å plotte flere kartlag i én figur, bruk ax parameteren for å spesifisere i hvilke akser data skal plottes.

Den enkleste måten å få en akse er å lagre den første plot()ens returverdi (se nedenfor). Et annet alternativ er å lage subplots(), muligens med bare en rad og en kolonne.

akser = bydeler.plot(facecolor="grey")
gamle_oslo.plot(ax=akser, facecolor="red")
adresser.plot(ax=akser, color="blue", markersize=5)

<Axes: >
../../_images/94bf8bc7e24e805cacb8dfe35985080f4317c034cd7bc0e2671617d50d34ddae.png

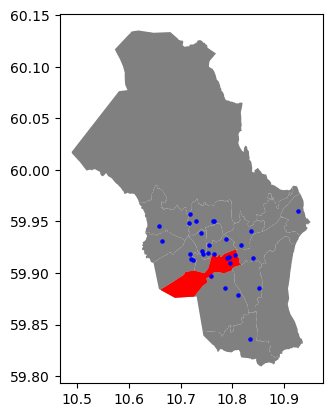
Noen punkter er innenfor ‘Gamle Oslo’, men andre er det ikke. For å finne ut hvilke som er de inne i bydelen, kan vi bruke en punkt-i-polygon spørring, denne gangen på en hel geopandas.GeoDataFrame. Metoden within() returnerer boolske (True/False) verdier som indikerer om eller ikke en rads geometri er inni den angitte andre geometrien:

geometri vs. geometrikolonne

I eksempelet nedenfor bruker vi gamle_oslo.at[0, "geometry"] for å få en enkelt verdi, et shapely.geometry.Polygon, i stedet for en hel kolonne (en GeoSeries). Dette er for å matche hver rad’s geometri av hele adresser-dataframen mot det samme polygonet. Hvis, i motsetning, vi ville kjøre within() mot en kolonne, ville operasjonen bli utført radvis, dvs. det første adressepunktet ville bli sjekket mot det første polygonet, det andre adressepunktet mot det andre polygonet, og så videre.

Sjekk dokumentasjonen for within() for å lære mer!

adresser.within(gamle_oslo.at[0, "geometry"])

0     False
1     False
2     False
3     False
4     False
5     False
6      True
7     False
8      True
9     False
10    False
11     True
12    False
13    False
14     True
15     True
16    False
17    False
18    False
19    False
20    False
21    False
22    False
23    False
24    False
25    False
26    False
27     True
28    False
29    False
dtype: bool

Denne listen med boolske verdier, også kalt en maske-array kan brukes til å filtrere input dataframen:

adresser_i_gamle_oslo = adresser[
    adresser.within(gamle_oslo.at[0, "geometry"])
]
adresser_i_gamle_oslo
fid address id adr geometry
6 7 5, Etterstadsletta, Gamle Oslo, Oslo, 0660, Norge 106 Etterstadsletta 5, 0660 OSLO POINT (10.79645 59.90968)
8 9 21, Fyrstikkalléen, Lilleberg, Gamle Oslo, Osl... 108 Fyrstikkalleen 21, 0661 OSLO POINT (10.79432 59.91526)
11 12 20B, Herslebs gate, Grønland, Gamle Oslo, Oslo... 111 Herslebs gate 20B, 0561 OSLO POINT (10.76403 59.91812)
14 15 30, Kongsveien, Grønlia, Gamle Oslo, Oslo, 019... 114 Kongsveien 30, 0193 OSLO POINT (10.75824 59.89739)
15 16 Gladengveien 3B, Gladengveien, Ensjø, Gamle Os... 115 Gladengveien 3B, 0661 OSLO POINT (10.7903 59.91467)
27 28 16G, Innspurten, Gullhaug, Gamle Oslo, Oslo, 0... 127 Innspurten 16, 0663 OSLO POINT (10.80587 59.91724)

Til slutt, la oss plotte denne listen med adresser en gang til for visuelt å verifisere at alle av dem, faktisk, er plassert i ‘Gamle Oslo’:

akser = bydeler.plot(facecolor="grey")
gamle_oslo.plot(ax=akser, facecolor="red")

adresser_i_gamle_oslo.plot(
    ax=akser,
    color="gold",
    markersize=5
)

<Axes: >
../../_images/72b22e43b43663b222e4b5ce681b9014ddf0a59dce16e279fb0e8da5bc76abf0.png

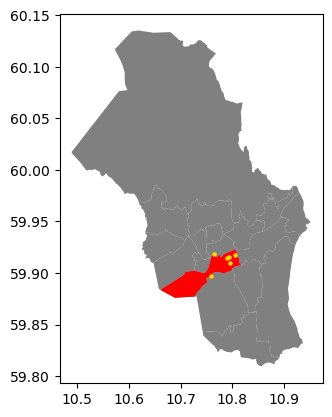
Perfekt! Nå sitter vi igjen med bare de (gyldne) punktene som faktisk er inne i det røde polygonet. Det er akkurat det vi ønsket!